![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: Review of the Single
Next: Results
Up: Single Gyre Circulation in
Figure 5.2:
The five geometries used for our application of the SE method.
The circle is deformed by super-imposition of a coastal
oscillation of the form of a sine wave. For Geometry V, we label
the bumps for later reference starting from the first bump west of the
north-south axis passing through the center of the basin and we then
proceed anticlockwise. The same labeling applies for the other
geometries.
|
|
In order to test these arguments, we consider the following experiment.
The set-up consists of wind-driven circulations in five different
geometries (Figure 5.2). The first is a circular geometry with the
radius given by Lc=500 km. The second is a perturbation of the first
geometry by the addition of a wavy pattern along the coastline in the form of a
sine wave. We choose the wave length to be a 1/16 of the perimeter. The
amplitude of the sine wave from a crest to a trough is 12.5 km. The third
geometry is the same one except that the amplitude of the sine perturbation is
25 km. The amplitude for the fourth and the fifth is respectively 50 and
100 km. The radius of curvature was computed using the simple relation:
 |
(5.8) |
where es and en are
the orthonormal unit vectors associated with the directions s and n. For a
sine wave given by
 the minimum radius of curvature is given
by
the minimum radius of curvature is given
by
 |
(5.9) |
In the context of
the circular geometry, we can correct the radius by using the relation:
 |
(5.10) |
Hence,
the minimum radius of curvature for the second geometry is about 160 km and
80 km, 40 km and 20 km for the third, fourth and fifth geometries. We use three
values of the eddy-viscosity ( 700, 300, 100 m2 s-2). The
wind-forcing is the same as applied in the previous chapter for single gyre
Munk problem. The Reynolds boundary number ranges therefore from 0.5 to 3.5. For
comparison, Scott and Straub (1998) reached impressive values of about 35 for
double gyre steady circulations with a QG model. In contrast, our maximum
achieved value of Re=3.5 is lower.
However, in the context of unsteady solutions in irregular geometries using a
shallow water reduced gravity model and due to our definition of VSv,
this can be considered a high value. The
inertial layer width is about 28 km whereas the viscous sublayer width varies
from 40 km to 15 km. Therefore, we expect that the processes are mostly
nonlinear. Since we are interested in the mean states of the circulation,
when possible, we
performed six year averages of the fields after
a statistical steady state has been reached. This period is limited by
computer resources.
It is a bit short since six years represent only twice the time for a Rossby
wave to cross the basin. However, we do not believe that these results would
significantly differ for longer averaging period.
700, 300, 100 m2 s-2). The
wind-forcing is the same as applied in the previous chapter for single gyre
Munk problem. The Reynolds boundary number ranges therefore from 0.5 to 3.5. For
comparison, Scott and Straub (1998) reached impressive values of about 35 for
double gyre steady circulations with a QG model. In contrast, our maximum
achieved value of Re=3.5 is lower.
However, in the context of unsteady solutions in irregular geometries using a
shallow water reduced gravity model and due to our definition of VSv,
this can be considered a high value. The
inertial layer width is about 28 km whereas the viscous sublayer width varies
from 40 km to 15 km. Therefore, we expect that the processes are mostly
nonlinear. Since we are interested in the mean states of the circulation,
when possible, we
performed six year averages of the fields after
a statistical steady state has been reached. This period is limited by
computer resources.
It is a bit short since six years represent only twice the time for a Rossby
wave to cross the basin. However, we do not believe that these results would
significantly differ for longer averaging period.
We first compare the results from the C-grid FD model using the promising
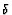 -
-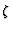 stress tensor formulation and the enstrophy conserving scheme (the B
combination of Section 4.22)
with those of the C-grid using the same
advective scheme and the conventional stress tensor formulation (the A
combination of Section 4.22).
Figure 5.3 shows the
elevation fields after a 3 year spin-up for
stress tensor formulation and the enstrophy conserving scheme (the B
combination of Section 4.22)
with those of the C-grid using the same
advective scheme and the conventional stress tensor formulation (the A
combination of Section 4.22).
Figure 5.3 shows the
elevation fields after a 3 year spin-up for
 100 m2 s-2. The
circulation of the B combination is much more inertial than the
circulation of the A combination. Furthermore (but not shown), the
vorticity fields are very noisy in both cases. The B combination run is
stopped
shortly after the third year of simulation because of the depletion of
the water column along the boundaries ($h<0$).
Figure 5.4
shows the total energy for both
combinations and the SE model. We consider the SE results to be the
``truth''. We note that the A combination is too dissipative and that the
B combination is not dissipative enough. The A combination is for this
geometry the combination closest to the SE results. That the B combination
is not dissipative enough can be related to the fact that this particular
configuration of the C-grid model specifies the vorticity to be zero at
the wall and therefore, does not take into account the influence of the
radius of curvature. Therefore, although the B combination was successful
in the presence of steps in a rectangular geometry (where free-slip implies
$\zeta=0$), this combination is no longer successful in the general case of
an irregular geometry where the vorticity can be non-zero at the walls.
A better way to implement the boundary condition in the FD model might be to
take into account the curvature of the boundary, as we do in the SE model.
This would require computing for each velocity node close to the boundary
a series of coefficients associated to nearby velocity points in order to
extrapolate the normal derivative of the tangential velocity
along the wall (i.e., a generalization of the off-centered two point
operator used in Section~\ref{app_sadourny} for enforcing free-slip along
straight walls.) The C-grid however does not easily allow for such an
implementation. One limitation comes from the fact that the velocity
components are not discretized at the same location. This implies
interpolations back and forth from the global coordinates to the local
curvilinear coordinates of the components of velocity. This sort of
two-way interpolation is damaging to the overall accuracy. Leakage of mass
from the computational domain is also a possibility that could affect the
accuracy.
We therefore need a model which represents more accurately the effects of
the walls. The SE model seems to be a good candidate. A second order FE
model, which satisfies the LBB stability condition and which is based on
the Eulerian time description, may be successful in this application as
well. However, from Chapter~3, the SE model would offer a robust and
faster convergence with increasing resolution at a more reasonable cost.
100 m2 s-2. The
circulation of the B combination is much more inertial than the
circulation of the A combination. Furthermore (but not shown), the
vorticity fields are very noisy in both cases. The B combination run is
stopped
shortly after the third year of simulation because of the depletion of
the water column along the boundaries ($h<0$).
Figure 5.4
shows the total energy for both
combinations and the SE model. We consider the SE results to be the
``truth''. We note that the A combination is too dissipative and that the
B combination is not dissipative enough. The A combination is for this
geometry the combination closest to the SE results. That the B combination
is not dissipative enough can be related to the fact that this particular
configuration of the C-grid model specifies the vorticity to be zero at
the wall and therefore, does not take into account the influence of the
radius of curvature. Therefore, although the B combination was successful
in the presence of steps in a rectangular geometry (where free-slip implies
$\zeta=0$), this combination is no longer successful in the general case of
an irregular geometry where the vorticity can be non-zero at the walls.
A better way to implement the boundary condition in the FD model might be to
take into account the curvature of the boundary, as we do in the SE model.
This would require computing for each velocity node close to the boundary
a series of coefficients associated to nearby velocity points in order to
extrapolate the normal derivative of the tangential velocity
along the wall (i.e., a generalization of the off-centered two point
operator used in Section~\ref{app_sadourny} for enforcing free-slip along
straight walls.) The C-grid however does not easily allow for such an
implementation. One limitation comes from the fact that the velocity
components are not discretized at the same location. This implies
interpolations back and forth from the global coordinates to the local
curvilinear coordinates of the components of velocity. This sort of
two-way interpolation is damaging to the overall accuracy. Leakage of mass
from the computational domain is also a possibility that could affect the
accuracy.
We therefore need a model which represents more accurately the effects of
the walls. The SE model seems to be a good candidate. A second order FE
model, which satisfies the LBB stability condition and which is based on
the Eulerian time description, may be successful in this application as
well. However, from Chapter~3, the SE model would offer a robust and
faster convergence with increasing resolution at a more reasonable cost.
Figure 5.3:
Elevation fields in the Geometry V for the C-grid model
after 3 years of spin-up.
On the left, the A Combination, on the right, the B combination.
|
|
|
|

|

|
Figure 5.3:
Total energy during spin-up for the A and B combinations of the FD
C-grid model and for the SE model at n_c=5 (SPOC~5) in Geometry V.
 100 m2 s-2.
100 m2 s-2.
|
|
|
|

|
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: Review of the Single
Next: Results
Up: Single Gyre Circulation in
Get the PS or PDF version here
Frederic Dupont
2001-09-11
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
![]() -
-![]() stress tensor formulation and the enstrophy conserving scheme (the B
combination of Section 4.22)
with those of the C-grid using the same
advective scheme and the conventional stress tensor formulation (the A
combination of Section 4.22).
Figure 5.3 shows the
elevation fields after a 3 year spin-up for
stress tensor formulation and the enstrophy conserving scheme (the B
combination of Section 4.22)
with those of the C-grid using the same
advective scheme and the conventional stress tensor formulation (the A
combination of Section 4.22).
Figure 5.3 shows the
elevation fields after a 3 year spin-up for
![]() 100 m2 s-2. The
circulation of the B combination is much more inertial than the
circulation of the A combination. Furthermore (but not shown), the
vorticity fields are very noisy in both cases. The B combination run is
stopped
shortly after the third year of simulation because of the depletion of
the water column along the boundaries ($h<0$).
Figure 5.4
shows the total energy for both
combinations and the SE model. We consider the SE results to be the
``truth''. We note that the A combination is too dissipative and that the
B combination is not dissipative enough. The A combination is for this
geometry the combination closest to the SE results. That the B combination
is not dissipative enough can be related to the fact that this particular
configuration of the C-grid model specifies the vorticity to be zero at
the wall and therefore, does not take into account the influence of the
radius of curvature. Therefore, although the B combination was successful
in the presence of steps in a rectangular geometry (where free-slip implies
$\zeta=0$), this combination is no longer successful in the general case of
an irregular geometry where the vorticity can be non-zero at the walls.
A better way to implement the boundary condition in the FD model might be to
take into account the curvature of the boundary, as we do in the SE model.
This would require computing for each velocity node close to the boundary
a series of coefficients associated to nearby velocity points in order to
extrapolate the normal derivative of the tangential velocity
along the wall (i.e., a generalization of the off-centered two point
operator used in Section~\ref{app_sadourny} for enforcing free-slip along
straight walls.) The C-grid however does not easily allow for such an
implementation. One limitation comes from the fact that the velocity
components are not discretized at the same location. This implies
interpolations back and forth from the global coordinates to the local
curvilinear coordinates of the components of velocity. This sort of
two-way interpolation is damaging to the overall accuracy. Leakage of mass
from the computational domain is also a possibility that could affect the
accuracy.
We therefore need a model which represents more accurately the effects of
the walls. The SE model seems to be a good candidate. A second order FE
model, which satisfies the LBB stability condition and which is based on
the Eulerian time description, may be successful in this application as
well. However, from Chapter~3, the SE model would offer a robust and
faster convergence with increasing resolution at a more reasonable cost.
100 m2 s-2. The
circulation of the B combination is much more inertial than the
circulation of the A combination. Furthermore (but not shown), the
vorticity fields are very noisy in both cases. The B combination run is
stopped
shortly after the third year of simulation because of the depletion of
the water column along the boundaries ($h<0$).
Figure 5.4
shows the total energy for both
combinations and the SE model. We consider the SE results to be the
``truth''. We note that the A combination is too dissipative and that the
B combination is not dissipative enough. The A combination is for this
geometry the combination closest to the SE results. That the B combination
is not dissipative enough can be related to the fact that this particular
configuration of the C-grid model specifies the vorticity to be zero at
the wall and therefore, does not take into account the influence of the
radius of curvature. Therefore, although the B combination was successful
in the presence of steps in a rectangular geometry (where free-slip implies
$\zeta=0$), this combination is no longer successful in the general case of
an irregular geometry where the vorticity can be non-zero at the walls.
A better way to implement the boundary condition in the FD model might be to
take into account the curvature of the boundary, as we do in the SE model.
This would require computing for each velocity node close to the boundary
a series of coefficients associated to nearby velocity points in order to
extrapolate the normal derivative of the tangential velocity
along the wall (i.e., a generalization of the off-centered two point
operator used in Section~\ref{app_sadourny} for enforcing free-slip along
straight walls.) The C-grid however does not easily allow for such an
implementation. One limitation comes from the fact that the velocity
components are not discretized at the same location. This implies
interpolations back and forth from the global coordinates to the local
curvilinear coordinates of the components of velocity. This sort of
two-way interpolation is damaging to the overall accuracy. Leakage of mass
from the computational domain is also a possibility that could affect the
accuracy.
We therefore need a model which represents more accurately the effects of
the walls. The SE model seems to be a good candidate. A second order FE
model, which satisfies the LBB stability condition and which is based on
the Eulerian time description, may be successful in this application as
well. However, from Chapter~3, the SE model would offer a robust and
faster convergence with increasing resolution at a more reasonable cost.



![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)