![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: Results
Next: Adaptivity
Up: Single Gyre Circulation in
Figure 5.18:
The region in grey represents where the absolute vorticity is
approximately conserved. It encloses the inertial layer along the
western boundary and the recirculation in the north-western corner.
|
|
In order to interpret the large scale and steady characteristics of the
Munk circulation of the previous sections, we propose to develop some
scaling arguments and compare these with the numerical results. One
approach is to derive a criterion based on vorticity budgets (following
Pedlosky) under the free-slip boundary condition for steady solutions
which allows for curved boundaries. For straight walls, the relative
vorticity is zero along the boundary. For a strong inertial layer in which
we neglect viscous effects, we know that the absolute vorticity
is conserved along a parcel trajectory (see
Figure 5.18). Let us consider the conservation of absolute
vorticity for simplicity. This one is
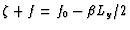 in
the southern part of the domain (upstream of the inertial layer) where the
relative vorticity is zero. Since absolute vorticity is conserved in the
inertial layer, it is reasonable to imagine that the minimum absolute
vorticity is such that
in
the southern part of the domain (upstream of the inertial layer) where the
relative vorticity is zero. Since absolute vorticity is conserved in the
inertial layer, it is reasonable to imagine that the minimum absolute
vorticity is such that
 in
the northern part of the domain (downstream of the inertial layer).
Therefore, the minimum relative vorticity is
in
the northern part of the domain (downstream of the inertial layer).
Therefore, the minimum relative vorticity is
 .
Hence,
in order to have an idea of the magnitude of the viscous flux of vorticity
out of the domain, we only need to estimate the width of the viscous
sublayer in the presence of the recirculation.
One limitation, though, of this
approximation is that the recirculation is formed of closed contours of
both potential vorticity and the streamfunction. Hence, to the extent that
particles remain trapped in the recirculation for long periods, wind
forcing can lead to even lower values of
.
Hence,
in order to have an idea of the magnitude of the viscous flux of vorticity
out of the domain, we only need to estimate the width of the viscous
sublayer in the presence of the recirculation.
One limitation, though, of this
approximation is that the recirculation is formed of closed contours of
both potential vorticity and the streamfunction. Hence, to the extent that
particles remain trapped in the recirculation for long periods, wind
forcing can lead to even lower values of 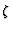 here. However, from
experience, the minimum in the recirculation zone is usually superior to
(less negative) or about the number we gave (
here. However, from
experience, the minimum in the recirculation zone is usually superior to
(less negative) or about the number we gave (
 ), as long as the
recirculation zone is confined to the northwestern part of the gyre. As
soon as this zone reaches the eastern walls (i.e., with increased Re),
it forms a Fofonoff-type gyre that fills the whole basin, and for which
the vorticity is much lower.
Using the vorticity budget given in (5.1) and the
viscous sublayer thickness,
), as long as the
recirculation zone is confined to the northwestern part of the gyre. As
soon as this zone reaches the eastern walls (i.e., with increased Re),
it forms a Fofonoff-type gyre that fills the whole basin, and for which
the vorticity is much lower.
Using the vorticity budget given in (5.1) and the
viscous sublayer thickness,
 ,
as the scale at which the
vorticity varies in the boundary layer, we derive the simple criterion for
a circulation in straight walls in the presence of a strong recirculation (
,
as the scale at which the
vorticity varies in the boundary layer, we derive the simple criterion for
a circulation in straight walls in the presence of a strong recirculation (
 ):
):
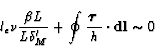 |
(5.17) |
where le is the length of the recirculation. The second term, the
wind input, in the vorticity balance is easy to determine. It varies with
h; however, from experience, we can consider 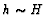 .
A first scaling for le can be obtained
from (5.17) after substituting (5.2-5.5):
.
A first scaling for le can be obtained
from (5.17) after substituting (5.2-5.5):
 |
(5.18) |
For Re=0.5, we obtain le=710 km, which is reasonably close to what is
observed in Figure 5.5.
This scaling can be compared to Pedlosky's (1996, pages 85-86). Pedlosky
evaluates the recirculation length scale using three equalities. The first
one comes from the equality in the momentum equations between the
advection terms and the diffusion terms in the viscous sublayer in the
presence of the recirculation:
 |
(5.19) |
where l* is the thickness of the sublayer and  is the transport in
the recirculation.
The second equality comes from the transport in the sublayer being equal
to the Sverdrup transport and from the velocity in the sublayer being
equivalent to the velocity at the edge of the recirculation:
is the transport in
the recirculation.
The second equality comes from the transport in the sublayer being equal
to the Sverdrup transport and from the velocity in the sublayer being
equivalent to the velocity at the edge of the recirculation:
 |
(5.20) |
The third equality comes from the vorticity input
by the wind in the interior of the ocean being equal to the viscous
flux of vorticity across the recirculation edge
 |
(5.21) |
These three combined equations allow one to derive one equation for le:
 |
(5.22) |
which can be simplified using (5.2-5.5) to
 |
(5.23) |
Pedlosky's scaling of le however implies an inconsistent definition of the
viscous boundary layer thickness along the recirculation. The thickness
for the viscous sublayer can be obtained from (5.19-5.23):
 |
(5.24) |
Using again (5.2-5.5),
this equation becomes
 |
(5.25) |
Hence, the viscous sublayer thickness is no longer dependent on  .
This seems counter-intuitive: for high Re, one expects
.
This seems counter-intuitive: for high Re, one expects
 .
Therefore, we will continue to use
our own estimate of
.
Therefore, we will continue to use
our own estimate of  as given in (5.5) and we will
give the equivalent result using
as given in (5.5) and we will
give the equivalent result using  in the presence of a
recirculation as given by Pedlosky. The true scaling might be in between
these two values. Nonetheless, in both cases, the behavior of le with
increasing Reynolds number is roughly the same. The recirculation length
quickly increases with increasing Reynolds number and the Sverdrup
interior can no longer be sustained for Re> 1.
in the presence of a
recirculation as given by Pedlosky. The true scaling might be in between
these two values. Nonetheless, in both cases, the behavior of le with
increasing Reynolds number is roughly the same. The recirculation length
quickly increases with increasing Reynolds number and the Sverdrup
interior can no longer be sustained for Re> 1.
Now, in the presence of a curved coastline,
(5.17) is modified to account for the positive vorticity
produced at the wall. Since the recirculation has closed contours of
streamlines, all the Sverdrup transport goes between the
recirculation and the wall. We assume this region to be the
viscous sublayer. Therefore, the volume transport through the sublayer is:
 |
(5.26) |
where v* is the velocity in the viscous sublayer (this is actually identical
to Eq. 5.20)). This yields
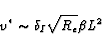 |
(5.27) |
for the scaling of v*. Using (5.26), we estimated v* to be
of the order of 0.84 m/s for Re=3.5. We now need to estimate the
vorticity produced at the wall. This is of the order of v*/Rs as given
by (5.7). Let us assume that the production of
positive vorticity is valid within
half a wavelength of the curvy coastline and
that no vorticity is produced in the other half. The second term in
(5.1) becomes
 |
(5.28) |
Therefore, in the presence of curved coastlines, the relation (5.17)
becomes:
 |
(5.29) |
Using the same values as above,
 at Re=0.5
and Rs=10 km, this relation yields a
length of le=340 km.
at Re=0.5
and Rs=10 km, this relation yields a
length of le=340 km.
There are two regimes, depending on the magnitude of Rs, the radius of
curvature of the coastline; one at low curvature corresponding to
(5.18) and the second at high curvature that we want to
investigate. Let us consider now the condition under which the
recirculation is controlled by the curvature of the coastline. This
condition corresponds to the second term being larger than the first term
in the denominator of (5.29):
 |
(5.30) |
and after substituting (5.5,5.26), we obtain
 |
(5.31) |
Hence, the transition depends on the Reynolds number. As Re increases,
the radius of curvature can increase for the second regime to persist,
implying less curvy
coastlines. For the second regime,
the length of the recirculation is governed by the vorticity produced at
the wall and, substituting (5.5,5.26), is scaled as
 |
(5.32) |
Hence, the length of the recirculation in curved geometries is no longer
dependent on the eddy-viscosity,  .
In other words, the Reynolds
number dependence in le disappears. This result is valid as long as the
curvature satisfies (5.31).
.
In other words, the Reynolds
number dependence in le disappears. This result is valid as long as the
curvature satisfies (5.31).
The weakest point in this argument is probably the estimate of the
thickness of the viscous sublayer ( )
and the velocity in the
sublayer (v*) in the presence of the recirculation. Using the estimation
of Pedlosky,
)
and the velocity in the
sublayer (v*) in the presence of the recirculation. Using the estimation
of Pedlosky,
 ,
we would have found
,
we would have found
 |
(5.33) |
By this estimation, le is still dependent on the Reynolds number, but
the dependence would be somewhat weaker when compared to regular domains
(Eq 5.18 or 5.23). Moreover, in the presence of curved
coastline, it is not clear what  becomes. The viscous sublayer
might be squeezed between the recirculation and the bumps and therefore,
the normal derivative of the vorticity might be increased, which favors
smaller recirculations. It is also possible that the viscous sublayer is not
squeezed but
that some streamlines of the recirculation may
lie within it. In such a case, a proper definition of the viscous
sublayer becomes difficult.
The second point relates to the form that the
vorticity takes around the bumps, which we assume to be constant over a
half wavelength of the curvy coastline.
As we noted in the numerical results, the vorticity
actually behaves quite singularly at the tip of bumps.
An additional
problem relates to the length of the perimeter which increases with
increasing number of bumps and with increasing amplitude of these bumps.
This would again favor lower values for le. Lastly, these scaling
arguments were based on the assumption that the action of the transient
eddies are
negligible, which may not be the case for sufficiently high Re.
becomes. The viscous sublayer
might be squeezed between the recirculation and the bumps and therefore,
the normal derivative of the vorticity might be increased, which favors
smaller recirculations. It is also possible that the viscous sublayer is not
squeezed but
that some streamlines of the recirculation may
lie within it. In such a case, a proper definition of the viscous
sublayer becomes difficult.
The second point relates to the form that the
vorticity takes around the bumps, which we assume to be constant over a
half wavelength of the curvy coastline.
As we noted in the numerical results, the vorticity
actually behaves quite singularly at the tip of bumps.
An additional
problem relates to the length of the perimeter which increases with
increasing number of bumps and with increasing amplitude of these bumps.
This would again favor lower values for le. Lastly, these scaling
arguments were based on the assumption that the action of the transient
eddies are
negligible, which may not be the case for sufficiently high Re.
We now compare the predictions from our scaling argument about the
recirculation length scale to Figure 5.5. We note
that, at Re=0.5, the recirculation changes in character between
Geometry II and III. Between these two geometries, the strength of the
recirculation weakens and its length decreases. Moreover, for Geometry V,
the length of the recirculation does not increase significantly with
increasing Re (300 km to 350 km). The latter observation is consistent
with (5.32). Therefore, the circulation seems to be controlled by
the curvature of the geometry between Geometry II and III. At Re=0.5,
the inequality (5.31) is however only satisfied for
Geometry V. Moreover, for a fixed radius of curvature,
(5.31) should be satisfied at a specific Re and the circulation in
that particular geometry should be controlled by the radius of curvature beyond
that specific Re.
However, we observe the opposite. For
example, as Re increases, the length of the recirculations for Geometry
IV increases slowly but then jumps to the energetically high branch.
The criterion (5.31) may not be very representative when the
solution tends to jump to the energetically high branch with increasing
Re. Nonetheless, the formula derived for le seems to yield a
relatively good prediction when the curvature is large enough (Geometry
V).
Figure 5.19:
Maximum of the mean elevation for the three geometries. The
maximum elevation is a good proxy for the strength of the recirculation.
|
|
Now focusing on results from Geometries I, IV and V, we derive
a predictive law for the strength of the recirculation based on previous
scalings. The Geometries IV and V are chosen because they show
the most robust sign that their circulation is controlled by the curvature.
The strength of the gyre is given by the maximum transport through the
basin (dominated by the recirculation).
Let us define the strength of the recirculation as the
volume transport through it. The transport is defined as the mean velocity
in the recirculation multiplied by its cross-section length.
Let us assume that the magnitudes of v* and le are
sufficient to characterize this transport.
From (5.18) and (5.27),
the maximum transport in regular basins is then given by
 |
(5.34) |
and in irregular basins by,
substituting (5.27) and (5.32)
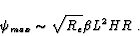 |
(5.35) |
Therefore the strength should be sensitive to the presence of the bumps.
A good proxy for the strength of the gyre is the maximum elevation
observed in the basin (because of the geostrophic approximation prevailing in
most of the domain).
Figure 5.19 shows the maximum elevation with respect to Re.
It appears that the strength of the gyre is dependent on the form of the
geometry. There is a clear shift in the strength of the gyre between
Geometries I and IV. Moreover, the slope (the power relation between hmand
Re or the slope coefficient in a log-log plot)
is close to unity for the regular
geometry (1.06), whereas it is about 0.5 for Geometry IV. At Re=0.5,
the
strength is identical for Geometry IV and V, but the slope is somewhat
less for Geometry V. These results seem to follow (5.34)
and (5.35), and the scaling for the sublayer thickness
in the presence of the recirculation seems therefore to be closer
to (5.5)
than to that of Pedlosky.
Figure 5.20:
Kinetic energy of the mean fields with respect to the boundary
Reynolds number. One point has been plotted on the high energy branch for
the first geometry. This one was evaluated using a FD-QG model in a
rectangular domain and is plotted only for giving the order of the jump.
|
|
Another important quantity related to the strength of the gyre is the
kinetic energy (KE). We plot KE with respect to Re.
Since the strength of the recirculation is dependent on the Reynolds
number via v*, the kinetic energy must depend on the Reynolds number
despite the presence of the indentations, but at much lower rate compared
to the kinetic energy in regular geometries. By assuming that, at first
order, KE is governed by the energy in the recirculation, we estimate
that in the
regular geometry the energy grows with both the length and the strength of
the recirculation by using (5.18) and (5.27)
 |
(5.36) |
whereas it grows only with the strength of the recirculation in the presence
of indentations, substituting (5.27) and (5.32)
 |
(5.37) |
Figure 5.20 shows the increase in the energy of the mean fields
for Geometries I, IV and V. The presence of a wavy perturbation of the
circular geometry retards the jump of the solution to the high energy
branch and the increase with the Reynolds number is much slower in the
presence of indentations along the coastline. Before the solution in the
intermediate geometry jumps to the high branch, it is noteworthy that the
slope for  with respect to
with respect to  ,
for the two irregular
geometries, is rather similar. The slope is 1.7 for Geometry I, and 0.85
for Geometry IV and 1.0 for V. All actual values for the slopes are rather
close to their expected values, even though this might be coincidental.
,
for the two irregular
geometries, is rather similar. The slope is 1.7 for Geometry I, and 0.85
for Geometry IV and 1.0 for V. All actual values for the slopes are rather
close to their expected values, even though this might be coincidental.
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: Results
Next: Adaptivity
Up: Single Gyre Circulation in
Get the PS or PDF version here
Frederic Dupont
2001-09-11
![\includegraphics[scale=0.3]{images/vort.eps}](Images/img429.gif)
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
![\includegraphics[scale=0.3]{images/vort.eps}](Images/img429.gif)
![]() in
the southern part of the domain (upstream of the inertial layer) where the
relative vorticity is zero. Since absolute vorticity is conserved in the
inertial layer, it is reasonable to imagine that the minimum absolute
vorticity is such that
in
the southern part of the domain (upstream of the inertial layer) where the
relative vorticity is zero. Since absolute vorticity is conserved in the
inertial layer, it is reasonable to imagine that the minimum absolute
vorticity is such that
![]() in
the northern part of the domain (downstream of the inertial layer).
Therefore, the minimum relative vorticity is
in
the northern part of the domain (downstream of the inertial layer).
Therefore, the minimum relative vorticity is
![]() .
Hence,
in order to have an idea of the magnitude of the viscous flux of vorticity
out of the domain, we only need to estimate the width of the viscous
sublayer in the presence of the recirculation.
One limitation, though, of this
approximation is that the recirculation is formed of closed contours of
both potential vorticity and the streamfunction. Hence, to the extent that
particles remain trapped in the recirculation for long periods, wind
forcing can lead to even lower values of
.
Hence,
in order to have an idea of the magnitude of the viscous flux of vorticity
out of the domain, we only need to estimate the width of the viscous
sublayer in the presence of the recirculation.
One limitation, though, of this
approximation is that the recirculation is formed of closed contours of
both potential vorticity and the streamfunction. Hence, to the extent that
particles remain trapped in the recirculation for long periods, wind
forcing can lead to even lower values of ![]() here. However, from
experience, the minimum in the recirculation zone is usually superior to
(less negative) or about the number we gave (
here. However, from
experience, the minimum in the recirculation zone is usually superior to
(less negative) or about the number we gave (
![]() ), as long as the
recirculation zone is confined to the northwestern part of the gyre. As
soon as this zone reaches the eastern walls (i.e., with increased Re),
it forms a Fofonoff-type gyre that fills the whole basin, and for which
the vorticity is much lower.
Using the vorticity budget given in (5.1) and the
viscous sublayer thickness,
), as long as the
recirculation zone is confined to the northwestern part of the gyre. As
soon as this zone reaches the eastern walls (i.e., with increased Re),
it forms a Fofonoff-type gyre that fills the whole basin, and for which
the vorticity is much lower.
Using the vorticity budget given in (5.1) and the
viscous sublayer thickness,
![]() ,
as the scale at which the
vorticity varies in the boundary layer, we derive the simple criterion for
a circulation in straight walls in the presence of a strong recirculation (
,
as the scale at which the
vorticity varies in the boundary layer, we derive the simple criterion for
a circulation in straight walls in the presence of a strong recirculation (
![]() ):
):
![]() )
and the velocity in the
sublayer (v*) in the presence of the recirculation. Using the estimation
of Pedlosky,
)
and the velocity in the
sublayer (v*) in the presence of the recirculation. Using the estimation
of Pedlosky,
![]() ,
we would have found
,
we would have found
![\includegraphics[scale=0.9]{images/cerc_hm.eps}](Images/img457.gif)
![\includegraphics[scale=0.9]{images/cerc_re.eps}](Images/img460.gif)
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)