![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: Presentation of the Numerical
Next: Finite Difference Models
Up: Presentation of the Numerical
Several time-stepping schemes are considered and used in conjunction with
one of the spatial discretization techniques proposed in the following
sections. For clarity, we review the time-stepping techniques separately
in this section. Let us consider the equation
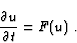 |
(2.3) |
The time-operator can be finite-differenced using a Taylor's series expansion
truncated after the first term:
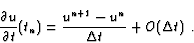 |
(2.4) |
The simplest time discretization consists then of integrating
(2.3) given the previous time-step fields. This formulation
corresponds to the so-called explicit forward Euler scheme and is only
first order accurate
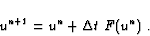 |
(2.5) |
This formulation is usually recommended for the integration of the
dissipative or friction terms, because no large precision is required in
time, as long as the small scale numerical noise are damped (and the
scheme is stable). For ensuring stability, a condition on the
magnitude of the time step, 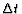 ,
applies. For instance, when
,
applies. For instance, when
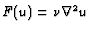 (a viscous dissipation term), this condition is
(a viscous dissipation term), this condition is
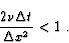 |
(2.6) |
Unfortunately, the forward Euler scheme is not neutral for various
problems, in the sense that some quantities such as mass, momentum or
energy are not conserved but may decay or grow as the simulation is
advanced in time. When these quantities grow with time, the model is of
course unstable. This happens, for instance, when F(u) represents the
Coriolis terms. In order to better conserve certain quantities, a better
scheme is the explicit leapfrog scheme
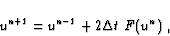 |
(2.7) |
based on a second order truncation
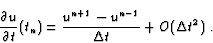 |
(2.8) |
The leapfrog scheme is thus centered in time. As the Euler
scheme, this scheme is restricted to certain conditions for stability.
For instance, if F(u)represents an advection or a wave propagation problem and using the
definition that the Courant number is given by
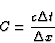 |
(2.9) |
where c is a phase speed
or an advection velocity, the CFL
(Courant-Friedrich-Levy) condition implies that
for stability. The Leapfrog scheme is neutral and conditionally stable
for problems involving, for instance, Coriolis or nonlinear advection
terms, and is unstable for dissipative terms. Moreover, the leapfrog
scheme requires a time-filtering, because the non-linearities and
round-off errors lead to a decoupling of the solution between even and odd
time steps. In order to avoid restriction of time-step magnitude, other
time-integrations techniques were introduced. They include implicit and
semi-implicit schemes. Nonetheless, these schemes have to respect a
certain condition on the Courant number for ensuring a good accuracy. The
semi-implicit 2.1 scheme
consists of
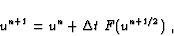 |
(2.11) |
where
F(un+1/2) = 1/2 ( F(un+1) +
F(un) ) and the fully-implicit scheme (also called the backward
Euler scheme) is implemented as
 |
(2.12) |
The advantage of the semi-implicit treatment is that the time-operator is
centered and second-order. For the Coriolis terms, the fully-implicit is
dissipative, and the semi-implicit (centered in time) is neutral. For the
treatment of the fast linear gravity waves present in the shallow water
equations, the advantage of using a semi-implicit or fully-implicit
technique is that there is no restriction on time-steps (the domain of
stability of the models is extended) but at the expense of solving a
matrix problem due to the coupling of the variables through partial
derivatives.
The disadvantage of
these two techniques is that some physical processes, such as gravity
waves, are slowed down if a too large time-step is used (i.e., C>1).
This may have consequences for the interactions of important dynamical
processes (the geostrophic and ageostrophic modes) and, therefore, this
may lead to a less accurate representation of the cascade of energy (as
mentioned in Bartello and Thomas, 1996).
The non-linear advective terms,
 ,
require a
special treatment. When we consider the computation of
,
require a
special treatment. When we consider the computation of
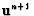 ,
they can be computed using the previous time step as
,
they can be computed using the previous time step as
 .
Then, if the time-operator is centered and leapfrog, the
non-linear terms are neutrally treated, otherwise, they are off-centered
for the other time-integration schemes and may be unstable or dissipative
depending on the time integration techniques. The non-linear terms can be
treated implicitly as
.
Then, if the time-operator is centered and leapfrog, the
non-linear terms are neutrally treated, otherwise, they are off-centered
for the other time-integration schemes and may be unstable or dissipative
depending on the time integration techniques. The non-linear terms can be
treated implicitly as
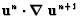 or fully implicit
using an iterative procedure. Another way is to use an explicit
4th order Adams-Bashforth formulation
or fully implicit
using an iterative procedure. Another way is to use an explicit
4th order Adams-Bashforth formulation
![\begin{displaymath}u^{n+1}= u^n + \frac{\Delta t}{12} \left[ 23 \; F(u^{n}) - 16 \; F(u^{n-1}) + 5 \; F(u^{n-2}) \right] \mbox{~.}
\end{displaymath}](Images/img58.gif) |
(2.13) |
The scheme is off-centered. It requires saving
fields from several previous time-steps and the time-step is limited by a
CFL condition. Use of Runge-Kutta techniques is also possible, the fourth
order one having the advantage of good quadratic conserving properties,
such as for the energy. But Runge-Kutta techniques require sub-step time
integrations as in this 4th order example:
 |
(2.14) |
The Runge-Kutta formulations are neutral for all phenomena, very
accurate, and require a CFL condition. Adams-Bashforth formulations are
usually recommended for non-linear integrations, but have the practical
disadvantage of requiring smaller time-steps than equivalent order
Runge-Kutta integrations, to the point that there is no definite advantage
of one technique over the other2.2. Hereafter, we tend to use the 4th order
Runge Kutta integration because of its accuracy and because it does not
require any time filtering.
A completely different time-stepping approach consists of using the
Lagrangian framework (the grid follows the particles) instead of the
Eulerian framework implicitly assumed previously (the grid is fixed in
time). The Lagrangian time-integration takes advantage of the fact that
the dynamical equations are simplified when written in a Lagrangian form
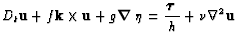 |
|
|
(2.15) |
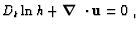 |
|
|
(2.16) |
where Dt is the Lagrangian or total time derivative.
This is another way of saying that the particle trajectory is the
characteristic line for the advective-only problem. Hence, the problematic
non-linear terms appearing in the equations do not appear explicitly
(except for the term in the mass balance). The main difficulty is in
following the particles that form the flow, and especially expressing the
right-hand-side terms. In order to avoid this problem, the so-called
semi-Lagrangian formulation was developed which takes advantage of both
the Lagrangian and Eulerian frameworks (see Staniforth and Côté, 1991,
for a review). The right-hand-side terms are discretized on
the Eulerian framework (in which derivatives are easy to express) and the
time-derivative is treated on the Lagrangian framework. The advantage is
in keeping a fixed grid or domain in time. An interpolation procedure is
used in order to transfer information from the Eulerian grid to the
Lagrangian grid (the particle trajectories). As the equations are
time-stepped along the advective characteristic lines (the particle
trajectories), there are no limitations imposed by numerical stability on
the magnitude of the time-step due to the advective terms. Therefore, the
method is effective in advection dominated flows. To be precise, according
to Bartello and Thomas (1996), the method is effective only if the
spectrum of energy is very steep (not too much energy at the smallest
scales). Moreover, a semi-implicit or fully-implicit method can be added
to the semi-Lagrangian treatment of the equations [Robert, 1981]. Thus
the model has virtually no limitations due to stability regarding
time-step magnitude with respect to any physical process described by the
momentum equations. However, the presence of orography is troublesome in
semi-Lagrangian methods, effectively reducing the allowable time-step
[Ritchie and Tanguay, 1996]. The advantage of using semi-Lagrangian methods in an
ocean where the topography is steep is, hence, unclear.
Since the equations are iterated in time, the interpolation can be very
damaging to the conservation properties of the flow (mass or energy). That
is why modelers have to use high order interpolation schemes (cubic or
more). Nonetheless, the interpolation technique is usually responsible for
a large numerical dissipation, difficult to minimize. On the other hand,
these models can run without explicit eddy-viscosity or diffusivity.
Proponents of the semi-Lagrangian method never fail to mention that their
models run without explicit numerical viscosity, whereas opponents note
that semi-Lagrangian models offer no control over this implicit viscosity.
Another disadvantage of the semi-Lagrangian technique when coupled to the
semi-implicit or implicit method is related to the same argument against
the semi-implicit and implicit methods. Namely, that too large a time-step
distorts the physical processes and misrepresents the real cascade of
energy.
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: Presentation of the Numerical
Next: Finite Difference Models
Up: Presentation of the Numerical
Get the PS or PDF version here
Frederic Dupont
2001-09-11
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
![]() ,
require a
special treatment. When we consider the computation of
,
require a
special treatment. When we consider the computation of
![]() ,
they can be computed using the previous time step as
,
they can be computed using the previous time step as
![]() .
Then, if the time-operator is centered and leapfrog, the
non-linear terms are neutrally treated, otherwise, they are off-centered
for the other time-integration schemes and may be unstable or dissipative
depending on the time integration techniques. The non-linear terms can be
treated implicitly as
.
Then, if the time-operator is centered and leapfrog, the
non-linear terms are neutrally treated, otherwise, they are off-centered
for the other time-integration schemes and may be unstable or dissipative
depending on the time integration techniques. The non-linear terms can be
treated implicitly as
![]() or fully implicit
using an iterative procedure. Another way is to use an explicit
4th order Adams-Bashforth formulation
or fully implicit
using an iterative procedure. Another way is to use an explicit
4th order Adams-Bashforth formulation

![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)