| (2.47) |
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
The first development of the spectral element (SE) method occurred in the early eighties [Patera, 1984]. The SE method allows for irregular geometries and high accuracy because of varying order polynomials inside quadrangles or triangles that form the mesh. The main distinction between the FE and SE methods stems from the type of basis functions used to approximate the model equations. In FE methods, the basis functions are usually constructed for one specific order of the scheme (they are derived from Lagrange interpolators on regular grids inside each element). They need to be recomputed as the order of the FE method is modified. In SE methods, the basis functions are hierarchical and follow easier rules of construction (for instance, they can be derived from Chebyshev or Legendre polynomials). As the order is augmented, the former set of basis functions is simply augmented by a new set of polynomials constructed from the previous set. Therefore, in SE methods, the order of approximation is user-dependent and can even vary from element to element. There seem to be numerical advantages in terms of matrix inversion in using the Chebyshev or Legendre polynomials instead of regularly spaced Lagrange interpolators. The latter lead to poorer conditioned matrices as the order of the scheme is augmented [Le Provost and Vincent, 1986]. As with the spectral method, the accuracy of SE method is exponential with increasing polynomial order. However, the SE method offers much higher flexibility in terms of geometrical representation. And, contrary to the spectral method for which Gibbs oscillations are prone to occur in under-resolved regions, in the SE method, one can easily increase the polynomial order (p-refinement) or the number of elements (h-refinement) in the underesolved regions. Using a polynomial order greater than two, we can also expect that SE methods are more accurate than conventional FD or FE methods, and that the convergence of the solution with increasing resolution is much faster.
We noted two applications in ocean modelling using quadrangular SE. The first by Ma ma93 and the second and more successful by Iskandarani and Haidvogel iskan95. Using quadrangles, it is relatively easy to construct an orthogonal basis of cardinal functions which greatly facilitates the computation of nonlinear terms and renders trivial the matrix problem to be solved, provided the equations are prognostic and solved explicitly in time (leapfrog, Adams-Bashforth, Runge-Kutta). One limitation, however, of using continuous basis functions for the primitive (or shallow water) variables is that for stability the maximum polynomial order for approximating pressure (or elevation) has to be lowered, compared to velocity [Iskandarani and Haidvogel, 1995]. Lowering the maximum polynomial order of one variable is similar to staggering the variables in space in finite difference methods and is also similar to satisfying the LBB condition for finite element methods (see previous section). On the other hand, the method leads to a large but sparse matrix problem if the equations are solved implicitly in time, or if a Helmholtz or Poisson-type of system has to be solved. The only disadvantage of using quadrangles compared to triangles comes from the difficulty of discretizing an irregular domain into quadrangles, the triangles offering more flexibility. Using triangles [Sherwin and Karniadakis, 1996], there is no orthogonal basis of cardinal functions. Therefore, a large matrix problem has to be solved at each time-step, even when the equations are discretized explicitly in time. Moreover, the computation of nonlinear terms requires a tedious transfer from the spectral coefficients to values at Gauss-like points, and back to the spectral space. However, in restricted applications, recent developments led to simpler and cheaper algorithms. Lomtev and Karniadakis lomtev99 (hereafter referred as LK) avoid the difficult problem of defining a set of continuous high order polynomials over triangles by reverting to a discontinuous formulation which leads to a local matrix problem in each element-triangle. This is only possible if all the equations are prognostic (as they are for shallow water models) and treated explicitly in time. Luckily, a hydrostatic Boussinesq ocean with a free-surface can be modeled using this simplified spectral element method. Furthermore, their model appears to be stable although the same set of basis functions is used for the velocity and pressure. Thus, their method does not comply to the LBB condition. Finally, this method allows for an easy implementation of a time-variable mesh that we introduce in Section 2.4.3.
The matrix problem to be solved in each element is rather small for
the order of the spectral element we choose to test (between 3 to 7).
Therefore, the constraint of orthogonality over the set of polynomials for
a cost-effective model is made less stringent. Thus, we introduced an
even simpler set of basis functions compared to LK by simply using a set
of products of Legendre polynomials with a triangular truncation.
| (2.47) |
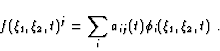 |
(2.48) |
| (2.50) |
![\includegraphics[scale=0.6]{images/tri1.eps}](Images/img144.gif) |
![\fbox{\raisebox{8em}{\rotatebox{-90}{
\includegraphics[scale=0.3]{images/legendre.eps}}}}](Images/img145.gif) |
We apply the discontinuous spectral element method to
the discretization of the shallow water equations.
Using a weak formulation and the traditional notation of Galerkin methods,
inside each element-triangle the system of equations reads:
The time integration is done using a 4th order Runge-Kutta method. Thus, using polynomials of degree nc=5 for instance, gives a certain equivalence between spatial and time truncation errors. The spectral element model is hereafter referred to as SPOC.
A constant eddy viscosity coefficient is used to allow for easy
comparisons
between models. In a discontinuous spectral element model, the Laplacian
operator of the velocity components cannot be computed directly (see LK
for details). The computation has to be done in two steps. First,
the gradient tensor of the velocity is computed using a weak formulation
and an integration by parts. The mass matrix is then inverted:
| (2.54) |
Given the two to three orders of magnitude difference between the scale of eddies and the basin scale, today's global ocean eddy resolving models require a variable in time and space resolution. To fulfill this constraint, not only do we need a variable in space resolution model (which the FE and SE models already offer), but we also need some flexibility of the mesh in time, since eddies and fronts are unsteady phenomena. By adaptive mesh refinement, we mean that the mesh is refined automatically as the simulation goes on in regions where estimated errors are the largest. The difficulty is in computing an error estimator that determines where to put more resolution. For FE methods using linear basis functions, it is usually recommended to estimate the local second order derivatives of the fields and put more resolution where these derivatives are the largest (Zienkiewicz and Taylor, 1991, p.571). Because the solution is piecewise linear, it is difficult to estimate its second order derivatives. This usually requires the reconstruction of the solution by a higher order method [Zhu and Zienkiewicz, 1990]. For continuous SE methods, adaptive strategies require to estimate the slope of the spectral coefficients with wave number. If there is too much energy in the high wave numbers, the elements have to be refined [Mavriplis, 1994]. This is a less complex procedure than that for FE methods. Adaptive strategies are difficult to implement in FD models because the Cartesian grids lack the flexibility of irregular meshes of FE and SE methods. Some adaptive mesh strategies have been proposed, though, in the form of nested grids. The coarse grid follows the overall circulation while the finer grid focuses on a particular region of interest. Both interacting in a one-way or two-way fashion depending on the models [Blayo and Debreu, 1999,Wadley and Bigg, 1999].
From the point of view of defining an error estimator, the discontinuous
SE method is slightly more effective. Since the proposed SE formulation
allows the solution to be discontinuous between elements, a
straightforward estimator is to compute the maximum jump between elements
for each field. Though very simple, this estimator has not yet been found
in the literature. This is therefore our own development. Once the error
estimator has been defined, the refinement or derefinement of the mesh is
fairly conventional and can be found in many textbooks, for instance in
Zienkiewicz and Taylor (1991) at p.574. We finally end up with four
parameters that control the refinement in time (see Table
2.2). The refinement is hierarchical. When a triangle is to
be refined, it is cut into four children-triangles and if the neighboring
triangles are not to be refined, they are cut into two children-triangles
in order to have a conformal connectivity. But if one of the two
children-triangles is to be later refined, their parent-triangle will be
cut into four, as the cutting into two children-triangles is only needed
to complete the connectivity (Fig.2.12). All the refinements of the
mesh will be kept in memory, easing the backward process of derefinement.
The CFL condition is updated every time the mesh is modified. The model
requires a certain adjustment time in order to smooth the jump between
elements after each refinement of the mesh. Therefore there is a minimum
value for ncheck (Table 2.2) depending on the time-step
and the physical parameters. Hence, for a time stepping simulation, the
model stops regularly to check the level of errors, refines the resolution
accordingly, interpolates the fields onto the new mesh and then restarts
with the new mesh and fields. In contrast to steady flows for which the
solution is unique (if the initial guess is close enough), the transient
simulations present the disadvantage that the solution accuracy might
degrade because the errors are still present in the new fields, although
the resolution has been improved. This justifies the use of ![]() ,
the relative jump value above which the errors have reached an
unacceptable level. If so, the model should not restart from the present
time-step but from a previously saved time-step at which the level of
errors was acceptable. The question of accuracy of adaptive time-stepping
solutions also arises from the issue of interpolating the variable fields,
since the interpolation does not conserve mass or energy.
,
the relative jump value above which the errors have reached an
unacceptable level. If so, the model should not restart from the present
time-step but from a previously saved time-step at which the level of
errors was acceptable. The question of accuracy of adaptive time-stepping
solutions also arises from the issue of interpolating the variable fields,
since the interpolation does not conserve mass or energy.
|
As we stressed in Section 2.2, the representation of the irregular geometry is the weakest point of FD methods. They represent the coastline as step-like walls. This would be equivalent to say that the boundary is piecewise constant, i.e, discontinuous. In contrast, FE methods usually represent a complex boundary by piecewise linear segments. Thus, the model boundary is C0 continuous. In order to represent accurately a complex boundary in SE formulations, it is better to stretch or curve the element boundaries than to increase the number of elements in a region of strong curvature (and keep the model boundary piecewise linear) as done in FE methods. Doing otherwise results in an increase in the number of elements and an increase in the resolution to the point that the cost of using higher order polynomials becomes prohibitive. It makes more sense to take advantage of the high order to get a boundary as smooth as possible (and try to get rid of discontinuities between piecewise segments along the boundary). This allows for faster convergence rates when the numerical solution is compared to analytical solutions found in continuously varying curvature domains. Furthermore, high order methods tend to behave badly in the presence of singularities along the boundaries (Gibbs oscillations). This is particularly true for this discontinuous SE method. In fact, we observe in one test-experiment these oscillations localized around the tip of one rectangular continent. Hence, a clear limitation of this SE formulation lies in the presence of singularities along the coastline. It is not so much a surprise that the high order methods tends to behave badly in the presence of singularities compared with low order methods. Singularities excite the highest modes of the high order methods and so, lead to strong oscillations. In particular, the adaptive method developed in the previous chapter fails to convergence in the presence of singularities (not shown). Therefore, the solution may come from smoothing out the geometry by using curved elements. In practice, the additional cost associated with the implementation of curved elements in triangular spectral elements limits the order of continuity of the model boundary. This section is devoted to the development of a curved spectral element model. Although curved spectral elements may appear natural, few details are available in the literature about their implementation. We therefore develop our own methodology.
For a triangle with local coordinates varying in
![]() ,
,
![]() ,
there is a local analytical transformation that
transforms one of the faces into a parabolic segment (Fig. 2.13):
,
there is a local analytical transformation that
transforms one of the faces into a parabolic segment (Fig. 2.13):
 |
(2.55) |
 |
(2.56) |
![\includegraphics[scale=0.7]{images/transtri1.eps}](Images/img167.gif)
|
 |
(2.57) |
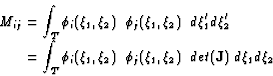 |
(2.58) |
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Get the PS or PDF version here