![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: an A-grid energy conserving
Next: Bibliography
Up: No Title
Using Equations 2.21 and 2.22, the model vorticity equation is obtained at the center of
the cell (also the  location):
location):
 |
(8.1) |
Study of this equation shows that all terms cancel out in the interior.
However, close to corners, they are not necessarily zero.
The pressure term, hereafter
IP, for
instance gives after summation over the domain and emphasizing the terms
close to the northeast corner (assuming
 ):
):
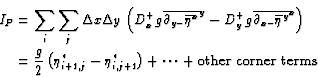 |
(8.2) |
where  is the extrapolated value of the elevation along the wall and
(i,j) are the indices taken at the velocity point directly southwest of
the corner. When
using a linear extrapolating law,
is the extrapolated value of the elevation along the wall and
(i,j) are the indices taken at the velocity point directly southwest of
the corner. When
using a linear extrapolating law,
 ,
IP becomes
,
IP becomes
 |
(8.3) |
Hence, the pressure term in the vorticity equation does not cancel out.
However, for the advective terms, hereafter Iadv, we have
 |
(8.4) |
which simplifies first to a circulation integral of the form
 |
(8.5) |
One can prove that this summation cancels out. Hence, Iadv=0. The same
occurs for the Coriolis terms because the summation can be recast as
a summation of flux normal to the
wall at velocity points along the wall,
which are zero due to the impermeability condition. Therefore, the model
vorticity budget reduces in the case of the B-grid to
 |
(8.6) |
Hence IP is present in the model budget whereas it should ideally be zero.
Note that a zero order extrapolation (
 )
results in
the cancellation of IP. However, this extrapolation leads
to countercurrents along the boundaries for the Munk problem on a beta plane, as
shown in Section 4.2.
)
results in
the cancellation of IP. However, this extrapolation leads
to countercurrents along the boundaries for the Munk problem on a beta plane, as
shown in Section 4.2.
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: an A-grid energy conserving
Next: Bibliography
Up: No Title
Get the PS or PDF version here
Frederic Dupont
2001-09-11
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
![]() location):
location):

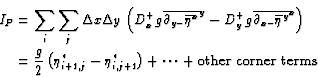


![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)