![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)
Previous: Contents
Next: List of Tables
Up: No Title
- Effect of the rotation on the discretization of a square domain.
- Effect of a poor resolution on the geometry of a strait.
- Elevation field for the Kelvin retardation problem in presence of steps
along the walls at two different resolutions.
- The three major horizontal staggerings for
the primitive equations.
- Triangulation of the domain.
 ,
the basis function related to the node Mi.
,
the basis function related to the node Mi.
 is the basis function related to the node x2=0.
is the basis function related to the node x2=0.
- The discontinuous linear non conforming basis function for
the
P1NC-P1 element of Hua and Thomasset hua84.
- The discontinuous constant basis function for pressure
over the macro-element of LLS.
- Local non-orthogonal coordinates in a given triangle
- Example of Legendre polynomials

- Remeshing strategies. The triangle to be refined is in grey.
- Transformation of one triangle intro a curved triangle
- Transformation of one triangle intro a curved triangle with
the coordinate system used in the computation of the
integrals
- The wave test experiment
- Convergence with resolution of the
normalized error in the u-component for second order C-grid formulation
(FDM), O-FDM4 and R-FDM4 models.
- CPU cost with the normalized error in u-component
for the second order C-grid
(FDM) and R-FDM4 models.
- The four FE models (LW, HT, PZM, LLS) are tested against the
analytical solution with increasing resolution.
- Convergence of the normalized error in
v with respect to the resolution for the LW-FE
and SE models
- Convergence of the normalized error in u with
respect to the resolution
for the C-grid FD, LW-FE
and SE models.
- Variation in the u-component normalized error as a function of CPU cost for
five models.
- Grids for the circular domain for the FD models.
- Convergence with resolution of the
normalized elevation error for the second order C-grid FD,
O-FDM4 and R-FDM4 models in a circular domain.
- Elevation error in a circular domain for four FE models.
- Normalized elevation error for the C-grid FD, LW-FE and
SE models for a circular domain.
- Total energy after 18 days of simulation for the
C-grid FD and the lumped LW, delumped LW, PZM and LLS FE models
and the SE model for the geostrophically balanced
eddy.
- Elevation field after a six year simulation in a non-rotated
basin using O-FDM4 and R-FDM4.
- As for Figure 3.13 but for rotated basin.
- Kinetic energy during a 6 year spin-up for the
C-grid FD, the lumped LW, HT, PZM and LLS
FE models.
- Elevation field after a 6 year spin-up for the
C-grid FD, the lumped LW, delumped LW,
HT, PZM and LLS FE models for the single gyre wind
forcing problem.
- Single gyre wind forcing experiments for the delumped LW FE model
compared to the C-grid FD model.
- Kinetic energy during spin-up for the
single gyre Munk problem with
 m2s-1 for
the C-grid FD, the delumped LW FE and SE models.
m2s-1 for
the C-grid FD, the delumped LW FE and SE models.
- Elevation field for the SE model after 6 years from spin-up for the
single gyre Munk problem with
 m2s-1,
nc=5.
m2s-1,
nc=5.
- As for Fig. 3.18
but with
 m2s-1.
m2s-1.
- As for Fig. 3.19
but with
 m2s-1.
m2s-1.
- Convergence with resolution for the nonlinear Munk problem
of the normalized kinetic energy error for the solution
from the C-grid FD and the SE models.
- As for Fig. 3.22 but for the
convergence of the normalized error with CPU cost.
- Solutions after a 6 year spin-up for the Munk problem using the
adaptive SE model with nc=5.
- Locations of variables near a step for the SW C-grid
model and the QG model.
- Local advective flux along the boundary at 20 km
resolution in a square basin for the enstrophy conserving
formulation.
- Northward flow past a forward step.
The shaded area is the model domain.
- Elevation fields in meters after a 6 year spin-up for 20 km and 10 km
resolution. Shown are results from the A and B combination with or without
a 3.44o rotation angle of the basin.
- (a) Kinetic energy after spin-up and (b)
ratio of
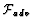 to
to
 for the four combinations
combinations.
for the four combinations
combinations.
-
Kinetic energy after spin-up for the B combination in
1010 m5/s2.
- Ratio of
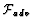 to
to
 for the B combination.
for the B combination.
-
Convergence of
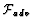 with
resolution for 0o, 20o, 45o rotation angle
for the B combination.
with
resolution for 0o, 20o, 45o rotation angle
for the B combination.
- Kinetic energy during spin-up for six runs
using the J1 Jacobian at 6 different rotation angles.
-
Kinetic energy after spin-up for
(a) J3 at 0o rotation,
(b) J7 at 0o,
(c) J3 at 30o,
(d) J7 at 30o,
(e) J3 at -30o,
(f) J7 at -30o.
- Ratio of
 to the wind input for
(a) J3 at 0o rotation,
(b) J7 at 0o,
(c) J3 at 30o,
(d) J7 at 30o.
to the wind input for
(a) J3 at 0o rotation,
(b) J7 at 0o,
(c) J3 at 30o,
(d) J7 at 30o.
- Ratio of
 to the wind input. (a-d) as
described in Fig. 4.10.
to the wind input. (a-d) as
described in Fig. 4.10.
-
Ratio of
 to the wind input. (a-d) as
described in Fig. 4.10.
to the wind input. (a-d) as
described in Fig. 4.10.
- Semi-advective flux, <
 , and beta contribution,
, and beta contribution,
 , to the
vorticity budget for the J3 Jacobian at -30o rotation angle.
, to the
vorticity budget for the J3 Jacobian at -30o rotation angle.
- Notation corresponding to the curvilinear coordinates.
- The five geometries used for our application of the SE method.
- Elevation fields in the Geometry V for the C-grid model
after 3 years of spin-up.
- Total energy during spin-up for the A and B combinations of the FD
C-grid model and for the SE model at nc=5 (SPOC 5) in Geometry V.
 m2s-1.
m2s-1.
- Mean elevation fields for the five geometries using the SE model.
- Mean vorticity field for the Geometries IV and V using the SE
model.
- Power input by the wind using the mean fields with respect to the
boundary Reynolds number.
- Mean standard deviation of the elevation.
- Mean standard deviation of the elevation for frequencies with
period above 200 days.
- Mean standard deviation of the elevation for frequencies with
period between 17 and 200 days.
- Mean standard deviation of the elevation for frequencies with
period between .6 and 17 days.
- Hovmöller diagram of the filtered elevation with respect to
time and location along the boundary.
- Amplitude of the Kelvin wave in meters along the boundary averaged
over 6 years.
- Time series of the amplitude of the oscillations at (x=500 km, y=0
km).
- Total energy for the last 6 years of simulation.
- Instantaneous vorticity field in the vicinity of the recirculation.
- (a) Local wind input to the vorticity in Geometry V.
(b) Local divergence of the eddy
transport of vorticity in Geometry V.
(c) Vector plot of the eddy transport of vorticity normal to the
streamlines in Geometry V.
- The region in grey represents where the absolute vorticity is
approximately conserved.
- Maximum of the mean elevation for the three geometries. The
maximum elevation is a good proxy for the strength of the recirculation.
- Kinetic energy of the mean fields with respect to the boundary
Reynolds number.
- Mesh for the original and the refined runs.
- Total energy for the last 6 years of simulation for the original
and refined meshes.
- Amplitude of the fast oscillations at (x=500 km, y=0 km) along the
boundary for the original and refined meshes.
- Mean elevation fields for the original mesh and the refined mesh.
- Mean vorticity fields for the original mesh and the refined mesh.
Frederic Dupont
2001-09-11
 ,
the basis function related to the node Mi.
,
the basis function related to the node Mi.
 is the basis function related to the node x2=0.
is the basis function related to the node x2=0.

 m2s-1 for
the C-grid FD, the delumped LW FE and SE models.
m2s-1 for
the C-grid FD, the delumped LW FE and SE models.
 m2s-1,
nc=5.
m2s-1,
nc=5.
 m2s-1.
m2s-1.
 m2s-1.
m2s-1.
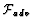 to
to
 for the four combinations
combinations.
for the four combinations
combinations.
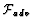 to
to
 for the B combination.
for the B combination.
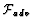 with
resolution for 0o, 20o, 45o rotation angle
for the B combination.
with
resolution for 0o, 20o, 45o rotation angle
for the B combination.
 to the wind input for
(a) J3 at 0o rotation,
(b) J7 at 0o,
(c) J3 at 30o,
(d) J7 at 30o.
to the wind input for
(a) J3 at 0o rotation,
(b) J7 at 0o,
(c) J3 at 30o,
(d) J7 at 30o.
 to the wind input. (a-d) as
described in Fig. 4.10.
to the wind input. (a-d) as
described in Fig. 4.10.
 to the wind input. (a-d) as
described in Fig. 4.10.
to the wind input. (a-d) as
described in Fig. 4.10.
 , and beta contribution,
, and beta contribution,
 , to the
vorticity budget for the J3 Jacobian at -30o rotation angle.
, to the
vorticity budget for the J3 Jacobian at -30o rotation angle.
 m2s-1.
m2s-1.
![[*]](Images/gaucheb.gif)
![[*]](Images/droiteb.gif)
![[*]](Images/hautb.gif)
![[*]](Images/tdm.gif)